20 Module NumPy

Le module NumPy est incontournable en bioinformatique. Il permet d'effectuer des calculs sur des vecteurs ou des matrices, élément par élément, via un nouveau type d'objet appelé array.

20.1 Installation et convention

Contrairement aux modules vus précédemment, NumPy n'est pas fourni avec la distribution Python de base. Avec la distribution Miniconda que nous vous conseillons d'utiliser (consultez pour cela la documentation en ligne), vous pouvez rapidement l'installer avec la commande :

$ conda install -c conda-forge numpy

Dans ce chapitre, nous vous montrerons quelques exemples d’utilisation du module NumPy pour vous convaincre de sa pertinence. Ces exemples seront exécutés dans un notebook Jupyter.

Les cellules de code apparaitront de cette manière
dans un notebook Jupyter, avec des numéros de lignes à gauche.

Les résultats seront affichés de cette manière,
éventuellement sur plusieurs lignes.

20.2 Chargement du module

On charge le module NumPy avec la commande :

import numpy

Par convention, on utilise np comme nom raccourci pour NumPy :

import numpy as np

20.3 Objets de type array

Les objets de type array correspondent à des tableaux à une ou plusieurs dimensions et permettent d'effectuer du calcul vectoriel. La fonction array() convertit un conteneur (comme une liste ou un tuple) en un objet de type array. Voici un exemple de conversion d'une liste à une dimension en objet array :

import numpy as np
a = [1, 2, 3]
np.array(a)

array([1, 2, 3])

b = np.array(a)
b

array([1, 2, 3])

type(b)

numpy.ndarray

Nous avons converti la liste [1, 2, 3] en array. La fonction np.array() accepte aussi comme argument un tuple, ou un objet de type range.

Par ailleurs, lorsqu'on demande à Python d'afficher le contenu d'un objet array, le mot array et les symboles ([ et ]) sont utilisés pour le distinguer d'une liste (délimitée par les caractères [ et ]) ou d'un tuple (délimité par les caractères ( et )).

Remarque

Un objet array ne contient que des données homogènes, c'est-à-dire d'un type identique. Il est possible de créer un objet array à partir d'une liste contenant des entiers et des chaînes de caractères, mais, dans ce cas, toutes les valeurs seront comprises par NumPy comme des chaînes de caractères :

a = np.array([1, 2, "tigre"])
a

array(['1', '2', 'tigre'], dtype='<U21')

Dans cet exemple, toutes les valeurs du array sont entre guillemets, indiquant qu'il s'agit de chaînes de caractères.

De même, il est possible de créer un objet array à partir d'une liste constituée d'entiers et de floats, mais toutes les valeurs seront alors comprises par NumPy comme des floats :

b = np.array([1, 2, 3.5])
b

array([1. , 2. , 3.5])

Ici, la notation 1. indique qu'il s'agit du float 1.0000... et pas de l'entier 1.

Sur un modèle similaire à la fonction range(), la fonction arange() permet de construire un array à une dimension :

np.arange(10)

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

Comme avec range(), on peut spécifier en argument une borne de début, une borne de fin et un pas :

np.arange(10, 0, -1)

array([10,  9,  8,  7,  6,  5,  4,  3,  2,  1])

Un autre avantage de la fonction arange() est qu'elle génère des objets array qui contiennent des entiers ou des floats (ce qui n'est pas possible avec range()) selon l'argument qu'on lui passe. D'abord un entier :

np.arange(10)

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

Puis un float :

np.arange(10.0)

array([ 0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9.])

La différence fondamentale entre un objet array à une dimension et une liste (ou un tuple) est que celui-ci est considéré comme un vecteur. Par conséquent, on peut effectuer des opérations vectorielles élément par élément sur ce type d'objet, ce qui est bien commode lorsqu'on analyse de grandes quantités de données. Regardez ces exemples :

v = np.arange(4)
v

array([0, 1, 2, 3])

On ajoute 1 à chacun des éléments de l'array v :

v + 1

array([1, 2, 3, 4])

On multiplie par 2 chacun des éléments de l'array v :

v * 2

array([0, 2, 4, 6])

Avec les listes, ces opérations n'auraient été possibles qu'en utilisant des boucles. Nous vous encourageons donc à utiliser dorénavant les objets array lorsque vous aurez besoin de faire des opérations élément par élément.

Il est aussi possible de multiplier deux arrays entre eux. Le résultat correspond alors à la multiplication élément par élément des deux arrays initiaux :

v * v

array([0, 1, 4, 9])

20.3.1 Array et dimensions

Il est aussi possible de construire des objets arrays à deux dimensions, il suffit de passer en argument une liste de listes à la fonction array() :

w = np.array([[1, 2], [3, 4], [5, 6]])
w

array([[1, 2],
       [3, 4],
       [5, 6]])

On peut aussi créer des tableaux à trois dimensions en passant comme argument à la fonction array() une liste de listes de listes :

x = np.array([[[1, 2], [2, 3]], [[4, 5], [5, 6]]])
x

array([[[1, 2],
        [2, 3]],

       [[4, 5],
        [5, 6]]])

La fonction array() peut créer des tableaux à n'importe quel nombre de dimensions. Toutefois, cela devient vite compliqué lorsqu'on dépasse trois dimensions. Retenez qu'un objet array à une dimension peut être assimilé à un vecteur, un array à deux dimensions à une matrice. On peut généraliser ces objets mathématiques avec un nombre arbitraires de dimensions, on parle alors de tenseur, qui sont représentés avec NumPy en array à \(n\) dimensions. Nous nous focaliserons dans la suite sur des arrays à une dimension (1D) ou deux dimensions (2D).

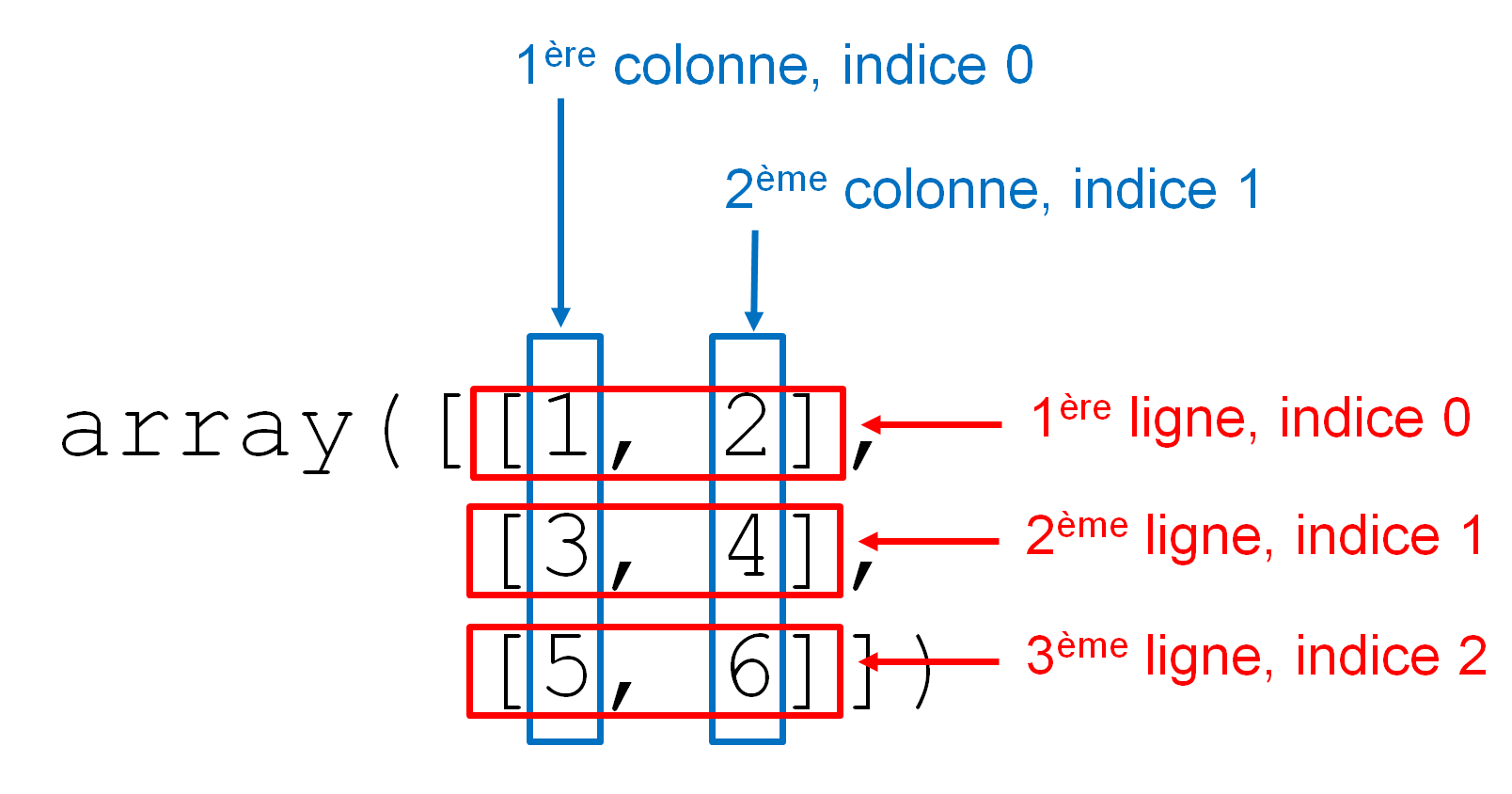
Avant de continuer, il est important de définir comment sont organisés ces arrays 2D qui représentent des matrices. Il s'agit de tableaux de nombres qui sont organisés en lignes et en colonnes comme le montre la figure 1. Les indices indiqués dans cette figure seront définis un peu plus loin dans la rubrique Indices.

Figure 1. Définition des lignes et colonnes dans un array 2D.

Voici quelques attributs intéressants pour décrire un objet array :

v = np.arange(4)
v

array([0, 1, 2, 3])

w = np.array([[1, 2], [3, 4], [5, 6]])
w

array([[1, 2],
       [3, 4],
       [5, 6]])

L'attribut .ndim renvoie le nombre de dimensions de l'array. Par exemple, 1 pour un vecteur et 2 pour une matrice :

v.ndim

1

w.ndim

2

L'attribut .shape renvoie les dimensions sous forme d'un tuple. Dans le cas d'une matrice (array à deux dimensions), la première valeur du tuple correspond au nombre de lignes et la seconde au nombre de colonnes.

v.shape

(4,)

w.shape

(3, 2)

Enfin, l'attribut .size renvoie le nombre total d'éléments contenus dans l'array :

v.size

4

w.size

6

20.3.2 Redimensionnement d'array

La méthode .reshape() renvoie un nouvel array avec les dimensions spécifiées en argument :

a = np.arange(0, 6)
a

array([0, 1, 2, 3, 4, 5])

a.shape

(6,)

b = a.reshape((2, 3))
b

array([[0, 1, 2],
       [3, 4, 5]])

b.shape

(2, 3)

a

array([0, 1, 2, 3, 4, 5])

Notez bien que l'array initial a n'a pas été modifié et que a.reshape((2, 3)) n'est pas la même chose que a.reshape((3, 2)) :

c = a.reshape((3, 2))
c

array([[0, 1],
       [2, 3],
       [4, 5]])

c.shape

(3, 2)

La méthode .reshape() attend que les nouvelles dimensions soient compatibles avec la dimension initiale de l'objet array, c'est-à-dire que le nombre d'éléments contenus dans les différents arrays soit le même. Dans nos exemples précédents, \(6 = 2 \times 3 = 3 \times 2\).

Si les nouvelles dimensions ne sont pas compatibles avec les dimensions initiales, la méthode .reshape() génère une erreur.

a = np.arange(0, 6)
a

array([0, 1, 2, 3, 4, 5])

a.shape

(6,)

d = a.reshape((3, 4))

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
Cell In[36], line 1
----> 1 d = a.reshape((3, 4))

ValueError: cannot reshape array of size 6 into shape (3,4)

La méthode .resize(), par contre, ne déclenche pas d'erreur dans une telle situation et ajoute des 0 jusqu'à ce que le nouvel array soit rempli, ou bien coupe la liste initiale :

a = np.arange(0, 6)
a.shape

(6,)

a.resize((3, 3), refcheck=False)
a.shape

(3, 3)

a

array([[0, 1, 2],
       [3, 4, 5],
       [0, 0, 0]])

b = np.arange(0, 10)
b.shape

(10,)

b.resize((2, 3), refcheck=False)
b.shape

(2, 3)

b

array([[0, 1, 2],
       [3, 4, 5]])

Attention

• Cette modification de la forme de l'array par la méthode .resize() est faite « sur place » (in place), c'est-à-dire que la méthode ne renvoie rien, mais l'array initial est bel et bien modifié (comme des méthodes sur les listes telles que la méthode .reverse(), voir le chapitre 13 Plus sur les listes).
• Si l'option refcheck=False n'est pas présente, Python peut parfois renvoyer une erreur s'il existe des références vers l'array qu'on souhaite modifier.

Enfin, il existe la fonction np.resize() qui, dans le cas d'un nouvel array plus grand que l'array initial, va répéter l'array initial afin de remplir les cases manquantes :

a = np.arange(0, 6)
a.shape

(6,)

c = np.resize(a, (3, 5))
c.shape

(3, 5)

c

array([[0, 1, 2, 3, 4],
       [5, 0, 1, 2, 3],
       [4, 5, 0, 1, 2]])

a

array([0, 1, 2, 3, 4, 5])

Notez que la fonction np.resize() renvoie un nouvel array mais ne modifie pas l'array initial, contrairement à la méthode .resize(), décrite ci-dessus.

Remarque

Depuis le début de ce chapitre, nous avons toujours montré l'affichage d'un array tel quel dans un notebook Jupyter :

a = np.array(range(10))
a

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

a2 = np.ones((3, 3))
a2

array([[1., 1., 1.],
       [1., 1., 1.],
       [1., 1., 1.]])

Nous avons déjà indiqué que Python affiche systématiquement le mot array ainsi que les parenthèses, crochets et virgules pour séparer les éléments. Toutefois, si vous utilisez la fonction print(), l'affichage sera différent. Le mot array, les parenthèses et les virgules disparaissent :

print(a)

[0 1 2 3 4 5 6 7 8 9]

print(a2)

[[1. 1. 1.]
 [1. 1. 1.]
 [1. 1. 1.]]

Ceci peut amener des confusions, en particulier entre un array 1D :

[0 1 2 3 4 5 6 7 8 9]

et une liste contenant les mêmes éléments :

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

Dans ce cas, seule la présence ou l'absence de virgules permet de savoir s'il s'agit d'un array ou d'une liste.

20.3.3 Méthodes de calcul sur les arrays et l'argument axis

Chaque array NumPy possède une multitude de méthodes. Nombre d'entre elles permettent de faire des calculs de base comme .mean() pour la moyenne, .sum() pour la somme, .std() pour l'écart-type, .max() pour extraire le maximum, .min() pour extraire le minimum, etc. La liste exhaustive est disponible en ligne. Par défaut, chacune de ces méthodes effectuera l'opération sur l'array entier, quelle que soit sa dimensionnalité. Par exemple :

import random
ma_liste = list(range(8))
random.shuffle(ma_liste)
ma_liste

[2, 7, 6, 4, 0, 3, 1, 5]

a = np.resize(ma_liste, (4, 2))
a

array([[2, 7],
       [6, 4],
       [0, 3],
       [1, 5]])

a.max()

7

La méthode .max() a bien renvoyé la valeur maximale 7. Un argument très utile existant dans toutes ces méthodes est axis. Pour un array 2D, axis=0 signifie qu'on fera l'opération le long de l'axe 0, à savoir les lignes. C'est-à-dire que l'opération se fait en variant les lignes. On récupère ainsi une valeur par colonne :

a.max(axis=0)

array([6, 7])

Dans l'array 1D récupéré, le premier élément vaut 6 (maximum de la 1ère colonne) et le second vaut 7 (maximum de la seconde colonne).

Avec axis=1, on fait une opération similaire, mais en faisant varier les colonnes. On récupère ainsi une valeur par ligne :

a.max(axis=1)

array([7, 6, 3, 5])

L'array 1D récupéré a quatre éléments correspondant au maximum de chaque ligne.

On comprend la puissance de l'argument axis. À nouveau, il est possible, en une ligne, de faire des calculs qui pourraient être fastidieux avec les listes traditionnelles.

20.3.4 Indices

Pour récupérer un ou plusieurs élément(s) d'un objet array, vous pouvez utiliser les indices, de la même manière qu'avec les listes :

a = np.arange(10)
a

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

a[1]

1

L'utilisation des tranches est aussi possible :

a[5:]

array([5, 6, 7, 8, 9])

Ainsi que les pas :

a[::2]

array([0, 2, 4, 6, 8])

Dans le cas d'un objet array à deux dimensions, vous pouvez récupérer une ligne complète (d'indice i), une colonne complète (d'indice j) ou bien un seul élément. La figure 1 montre comment sont organisés les indices des lignes et des colonnes :

a = np.array([[1, 2], [3, 4]])
a

array([[1, 2],
       [3, 4]])

a[:,0]

array([1, 3])

a[0,:]

array([1, 2])

La syntaxe a[i,:] renvoie la ligne d'indice i, et a[:,j] renvoie la colonne d'indice j. Les tranches sont aussi utilisables sur un array à deux dimensions.

a[1, 1]

4

La syntaxe a[i, j] renvoie l'élément à la ligne d'indice i et à la colonne d'indice j. Notez que NumPy suit la convention mathématiques des matrices, à savoir, qu'on définit toujours un élément par sa ligne puis par sa colonne. En mathématiques, l'élément \(a_{ij}\) d'une matrice \(A\) se trouve à la \(i^{ème}\) ligne et à la \(j^{ème}\) colonne :

Remarque

Pour un array 2D, si un seul indice est donné, par exemple a[i], on récupère la ligne d'indice i sous forme d'array 1D :

a = np.array([[1, 2], [3, 4]])
a

array([[1, 2],
       [3, 4]])

a[0]

array([1, 2])

a[1]

array([3, 4])

Pour cette raison, la syntaxe a[i][j] est également valide pour récupérer un élément :

a[1, 1]

4

a[1][1]

4

Nous vous recommandons la syntaxe a[i, j], qui est plus proche de la définition mathématique d'un élément de matrice.

20.3.5 Copie d'arrays

Comme pour les listes, nous attirons votre attention sur la copie d'arrays :

a = np.arange(5)
a

array([0, 1, 2, 3, 4])

b = a
b[2] = -300
b

array([   0,    1, -300,    3,    4])

a

array([   0,    1, -300,    3,    4])

Attention

Par défaut la copie d'arrays se fait par référence, comme pour tous les conteneurs en Python (listes, tuples, dictionnaires, etc.).

Afin d'éviter le problème, vous pouvez soit utiliser la fonction np.array(), qui crée une nouvelle copie distincte de l'array initial, soit la fonction copy.deepcopy(), comme pour les listes (voir chapitre 12 Plus sur les listes) :

a = np.full((2, 2), 0)
a

array([[0, 0],
       [0, 0]])

b = np.array(a)
b[1, 1] = -300
import copy
c = copy.deepcopy(a)
c[1, 1] = -500
a

array([[0, 0],
       [0, 0]])

b

array([[   0,    0],
       [   0, -300]])

c

array([[   0,    0],
       [   0, -500]])

La fonction np.full() est expliquée dans la rubrique suivante.

Remarque

L'instruction b = np.array(a) réalise bien une copie distincte de l'array a, quelle que soit sa dimensionnalité. Ceci n'était pas le cas avec la fonction list() pour les copies de listes à partir de la dimension deux (liste de listes) :

liste_1 = [[0, 0], [1, 1]]
liste_2 = list(liste_1)
import copy
liste_3 = copy.deepcopy(liste_1)
liste_1[1][1] = -365
liste_2

[[0, 0], [1, -365]]

liste_3

[[0, 0], [1, 1]]

20.4 Construction automatique de matrices

Il est parfois pénible de construire une matrice (array à deux dimensions) à l'aide d'une liste de listes. Le module NumPy possède quelques fonctions pratiques pour initialiser des matrices. Par exemple, Les fonctions zeros() et ones() construisent des objets array contenant des 0 ou des 1. Il suffit de leur passer en argument un tuple indiquant les dimensions voulues :

np.zeros((2, 3))

array([[0., 0., 0.],
       [0., 0., 0.]])

np.ones((3, 3))

array([[1., 1., 1.],
      [1., 1., 1.],
      [1., 1., 1.]])

Par défaut, les fonctions zeros() et ones() génèrent des floats, mais vous pouvez demander des entiers en passant le type (par exemple int, float, etc.) en second argument :

np.zeros((2,3), int)

array([[0, 0, 0],
       [0, 0, 0]])

Enfin, si vous voulez construire une matrice avec autre chose que des 0 ou des 1, vous avez à votre disposition la fonction full() :

np.full((2, 3), 7, int)

array([[7, 7, 7],
       [7, 7, 7]])

np.full((2, 3), 7, float)

array([[ 7.,  7.,  7.],
       [ 7.,  7.,  7.]])

Nous construisons ainsi une matrice constituée de 2 lignes et 3 colonnes. Celle-ci ne contient que le chiffre 7 sous formes d'entiers (int) dans le premier cas et de floats dans le second.

20.5 Chargement d'un array depuis un fichier

Le module NumPy contient aussi des fonctions pour lire des données à partir de fichiers et créer des arrays automatiquement. C'est très pratique, car la plupart du temps les données que l'on analyse proviennent de fichiers. La fonction la plus simple à prendre en main est np.loadtxt(). Celle-ci lit un fichier organisé en lignes et colonnes. Par exemple, imaginons que nous ayons un fichier donnees.dat contenant :

  1   7 310
 15  -4  35
 78  95  79

La fonction prend en argument le nom du fichier et renvoie un array 2D directement :

np.loadtxt("donnees.dat")

array([[  1.,   7., 310.],
       [ 15.,  -4.,  35.],
       [ 78.,  95.,  79.]])

Pratique, non ? Attention toutefois aux points suivants :

• Chaque ligne doit avoir le même nombre de colonnes, la fonction ne gère pas les données manquantes.
• Chaque donnée est convertie en float, donc si une chaîne de caractères est rencontrée la fonction renvoie une erreur.
• Par défaut, les données doivent être séparées par n'importe quelle combinaison d'espace(s) et/ou de tabulations.

Nous vous conseillons de consulter la documentation complète de cette fonction. En effet, np.loadtxt() contient de nombreux arguments permettant de récupérer telles ou telles lignes ou colonnes, d'ignorer des lignes de commentaire, de changer le séparateur par défaut (par exemple la virgule , pour les fichiers .csv)... qui peuvent se révéler utiles.

L'opération inverse qui consiste à sauver un array dans un fichier se fait avec la fonction np.savetxt() :

a = np.reshape(range(1, 10), (3, 3))
a

array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

np.savetxt("out.dat", a)

Ceci générera le fichier out.dat contenant les lignes suivantes :

1.000000000000000000e+00 2.000000000000000000e+00 3.000000000000000000e+00
4.000000000000000000e+00 5.000000000000000000e+00 6.000000000000000000e+00
7.000000000000000000e+00 8.000000000000000000e+00 9.000000000000000000e+00

La fonction np.savetxt() écrit par défaut les données comme des floats en notation scientifique. Il existe de nombreuses options possibles permettant de changer le format, les séparateurs, etc.

Pour aller plus loin

Il existe d'autres fonctions plus avancées telles que np.genfromttxt(), gérant les données manquantes, ou encore np.load() et np.fromfile(), permettant de lire des données au format binaire. De même, il existe des fonctions ou méthodes permettant d'écrire au format binaire : np.save() ou .tofile(). Le format binaire possède en général l'extension .npy ou .npz lorsque les données sont compressées. L'avantage d'écrire au format binaire est que cela prend moins de place pour de gros tableaux de données.

20.6 Concaténation d'arrays

Il peut être très utile de concaténer un ou plusieurs arrays. Il existe pour cela plusieurs fonctions dans NumPy, nous développerons celle qui nous parait la plus intuitive et directe : np.concatenate().

Pour les arrays 1D, np.concatenate() prend en argument un tuple contenant les arrays à concaténer :

a1 = np.array((0, 1))
a2 = np.array((3, 4))
a1

array([0, 1])

a2

array([3, 4])

np.concatenate((a1, a2))

array([0, 1, 3, 4])

L'ordre de la concaténation est important :

np.concatenate((a2, a1))

array([3, 4, 0, 1])

np.concatenate((a1, a2, a1, a2))

array([0, 1, 3, 4, 0, 1, 3, 4])

Pour les arrays 2D, ça se complique un peu, car on peut concaténer des lignes ou des colonnes ! Ainsi, np.concatenate() prend un argument optionnel, à savoir axis. Comme nous l'avions expliqué plus haut, celui-ci va indiquer à NumPy si on veut concaténer le long de l'axe 0 (les lignes) ou le long de l'axe 1 (les colonnes). Voyons un exemple :

a1 = np.reshape(np.array(range(6)), (3, 2))
a2 = a1 * 5
a1

array([[0, 1],
       [2, 3],
       [4, 5]])

a2

array([[ 0,  5],
       [10, 15],
       [20, 25]])

On concatène d'abord par ligne (axis=0), c'est-à-dire qu'on ajoute les lignes du second array a2 à celles de l'array a1 :

np.concatenate((a1, a2), axis=0)

array([[ 0,  1],
       [ 2,  3],
       [ 4,  5],
       [ 0,  5],
       [10, 15],
       [20, 25]])

Ensuite, on concatène par colonne (axis=1). Attention, il vaut bien veiller à ce que la concaténation soit possible en terme de dimensionalité. Par exemple, lors de la concaténation par colonne, il faut que les deux arrays a1 et a2 aient le même nombre de lignes :

np.concatenate((a1, a2), axis=1)

array([[ 0,  1,  0,  5],
       [ 2,  3, 10, 15],
       [ 4,  5, 20, 25]])

Ces opérations de concaténation sont très importantes. On les utilise par exemple si on a des données dans plusieurs fichiers différents et qu'on veut les agréger dans un array unique. On verra qu'on peut faire le même genre de chose avec les fameux Dataframes du module pandas. Lisez bien également les recommandations dans la dernière rubrique 17.1.10 Quelques conseils sur quand utiliser la concaténation d'arrays avec NumPy.

20.7 Un peu d'algèbre linéaire

Après avoir manipulé les objets array comme des vecteurs et des matrices, voici quelques fonctions pour faire de l'algèbre linéaire.

La fonction transpose() renvoie la transposée d'un array. Par exemple, pour une matrice :

a = np.resize(np.arange(1, 10), (3, 3))
a

array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

np.transpose(a)

array([[1, 4, 7],
       [2, 5, 8],
       [3, 6, 9]])

Tout objet array possède un attribut .T qui contient la transposée, il est ainsi possible d'utiliser cette notation objet plus compacte :

a.T

array([[1, 4, 7],
       [2, 5, 8],
       [3, 6, 9]])

La fonction dot() permet de multiplier deux matrices :

a = np.resize(np.arange(4), (2, 2))
a

array([[0, 1],
       [2, 3]])

np.dot(a, a)

array([[ 2,  3],
       [ 6, 11]])

a * a

array([[0, 1],
       [4, 9]])

Notez bien que dot(a, a) renvoie le produit matriciel entre deux matrices, alors que l'opération a * a renvoie le produit élément par élément.

Remarque

Dans le module NumPy, il existe également des objets de type matrix pour lesquels les multiplications de matrices sont différents, mais nous ne les aborderons pas ici.

Pour toutes les opérations suivantes, nous utiliserons des fonctions du sous-module linalg de NumPy.

La fonction diag() permet de générer une matrice diagonale :

a = np.diag((1, 2, 3))
a

array([[1, 0, 0],
       [0, 2, 0],
       [0, 0, 3]])

La fonction inv() renvoie l'inverse d'une matrice carrée :

np.linalg.inv(a)

array([[1.        , 0.        , 0.        ],
       [0.        , 0.5       , 0.        ],
       [0.        , 0.        , 0.33333333]])

La fonction det() renvoie le déterminant d'une matrice carrée :

np.linalg.det(a)

6.0

Enfin, la fonction eig() renvoie les vecteurs et valeurs propres :

np.linalg.eig(a)

EigResult(eigenvalues=array([1., 2., 3.]), eigenvectors=array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]]))

La fonction eig() renvoie un objet EigResult, qui contient les valeurs propres (eigenvalues) et les vecteurs propres (eigenvectors), qu'on peut ensuite récupérer par affectation multiple :

eigvals, eigvecs = np.linalg.eig(a)
eigvals

array([1., 2., 3.])

eigvals est un array 1D contenant les trois valeurs propres.

eigvecs

array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])

eigvecs est un array 2D contenant les trois vecteurs propres (un par ligne).

20.8 Parcours de matrice et affectation de lignes et colonnes

Lorsqu'on a une matrice, on est souvent amené à la parcourir par ligne ou par colonne. NumPy permet d'itérer directement sur les lignes d'une array :

a = np.reshape(np.arange(1, 10), (3, 3))
a

array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

for row in a:
    print(row, type(row))

[1 2 3] <class 'numpy.ndarray'>
[4 5 6] <class 'numpy.ndarray'>
[7 8 9] <class 'numpy.ndarray'>

À chaque itération, la variable row est un array 1D correspondant à chaque ligne de la matrice a. Cela est du au fait que l'utilisation d'un indiçage unique a[i] pour un array 2D correspond à sa ligne d'indice i (voir la rubrique Indices ci-dessus).

Pour itérer sur les colonnes, on peut utiliser l'astuce d'itérer sur la transposée de l'array a, c'est-à-dire a.T :

for col in a.T:
    print(col, type(col))

[1 4 7] <class 'numpy.ndarray'>
[2 5 8] <class 'numpy.ndarray'>
[3 6 9] <class 'numpy.ndarray'>

À chaque itération, la variable col est un array 1D correspondant à chaque colonne de a.

On se souvient de l'affectation multiple x, y = 1, 2 qui permettait d'affecter des valeurs à plusieurs variables à la fois. Il est possible d'utiliser cette fonctionnalité aussi avec les arrays NumPy :

a

array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

a1, a2, a3 = a
a1

array([1, 2, 3])

a2

array([4, 5, 6])

a3

array([7, 8, 9])

Par défaut, l'affectation multiple se fait sur les lignes de l'array 2D. Cette fonctionnalité s'explique à nouveau par le fait que pour NumPy, a[i] correspond à la ligne d'indice i d'un array 2D.

Pour utiliser l'affectation multiple sur les colonnes, il suffit d'utiliser la transposée a.T :

c1, c2, c3 = a.T
c1

array([1, 4, 7])

c2

array([2, 5, 8])

c3

array([3, 6, 9])

20.9 Masques booléens

Une fonctionnalité puissante des arrays NumPy est l'utilisation des masques booléens. Avant de les définir, il est important d'introduire le concept d'arrays de booléens. Jusqu'à maintenant nous avions définis uniquement des arrays avec des types numériques int ou float. Il est tout à fait possible de définir des arrays de booléens. La fonction np.full() vue précédemment nous permet d'en construire facilement :

np.full((2, 2), True)

array([[ True,  True],
       [ True,  True]])

np.full((2, 2), False)

array([[False, False],
       [False, False]])

Au premier abord, nous n'en voyons pas forcément l'utilité... Mais qu'en est-il lorsqu'on utilise les opérateurs de comparaison avec un array ? Et bien cela renvoie un array de booléens !

a = np.reshape(np.arange(1, 10), (3, 3))
a

array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

a > 5

array([[False, False, False],
       [False, False,  True],
       [ True,  True,  True]])

a == 2

array([[False,  True, False],
       [False, False, False],
       [False, False, False]])

Tous les éléments de l'array satisfaisant la condition seront à True, les autres à False. Il est même possible de combiner plusieurs conditions avec les opérateurs logiques & et | (respectivement ET et OU) :

a = np.reshape(np.arange(1, 10), (3, 3))
a

array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

(a > 3) & (a % 2 == 0)

array([[False, False, False],
       [ True, False,  True],
       [False,  True, False]])

(a > 3) | (a % 2 == 0)

array([[False,  True, False],
       [ True,  True,  True],
       [ True,  True,  True]])

• Les opérateurs logiques & et | s'appliquent sur les arrays et sont différents des opérateurs logiques and et or, qui eux s'appliquent sur les booléens (True ou False).
• Il est conseillé de mettre entre parenthèses chaque condition afin d'éviter les ambiguïtés.

Maintenant que les arrays de booléens ont été introduits, nous pouvons définir les masques booléens :

Définition

Les masques booléens sont des arrays de booléens qui sont utilisés en tant qu'« indice » d'un array initial. Cela permet de récupérer ou de modifier une partie de l'array initial.

Concrètement, il suffira d'utiliser un array et un opérateur de comparaison entre les crochets qui étaient dédiés à l'indiçage :

a = np.reshape(np.arange(1, 10), (3, 3))
a

array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

Pour isoler tous les éléments de l'array a qui sont supérieurs à 5 :

a[a > 5]

array([6, 7, 8, 9])

Pour isoler tous les éléments de l'array a qui sont égaux à 2 :

a[a == 2]

array([2])

Pour isoler tous les éléments de l'array a qui sont non nuls :

a[a != 0]

array([1, 2, 3, 4, 5, 6, 7, 8, 9])

À chaque fois, on ne récupère que les éléments de l'array a qui satisfont la sélection. Toutefois, il est important de remarquer que l'array renvoyé perd la dimensionnalité de l'array a initial, il s'agit systématiquement d'un array 1D.

La grande puissance de ce mécanisme est que l'on peut utiliser les masques booléens pour modifier les éléments que l'on sélectionne :

a = np.reshape(np.arange(1, 10), (3, 3))
a

array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

On sélectionne les éléments de l'array a supérieurs à 5 :

a[a > 5]

array([6, 7, 8, 9])

On affecte la valeur -1 aux éléments de l'array a supérieurs à 5 :

a[a > 5] = -1
a

array([[ 1,  2,  3],
       [ 4,  5, -1],
       [-1, -1, -1]])

On peut bien sûr combiner plusieurs conditions avec les opérateurs logiques :

a = np.reshape(np.arange(1, 10), (3, 3))
a

array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

a[(a > 3) | (a % 2 == 0)] = 0
a

array([[1, 0, 3],
       [0, 0, 0],
       [0, 0, 0]])

Ce mécanisme de sélection avec des masques booléens se révèle très puissant pour manipuler de grandes quantités de données. On verra qu'il peut être également utilisé avec les Dataframes du module pandas.

Remarque

Les masques booléens ne doivent pas être confondus avec les masked arrays, qui sont des arrays dans lesquels on peut trouver des valeurs manquantes ou invalides.

Enfin, une application possible des masques est de « binariser » une matrice de nombre :

import random
import numpy as np
a = np.resize([random.random() for i in range(16)], (4, 4))
a

array([[0.58704728, 0.50212977, 0.70652863, 0.24158108],
       [0.93102132, 0.41864373, 0.45807961, 0.98288744],
       [0.48198211, 0.16877376, 0.14431518, 0.74784176],
       [0.92913469, 0.08383269, 0.10670144, 0.14554345]])

seuil = 0.3
a[a < seuil] = 0
a[a > seuil] = 1
a

array([[1., 1., 1., 0.],
       [1., 1., 1., 1.],
       [1., 0., 0., 1.],
       [1., 0., 0., 0.]])

On obtient ce résultat avec deux lignes de code en utilisant des arrays, alors qu'il aurait fallu faire des boucles avec des listes classiques.

20.10 Quelques conseils

Nous vous avons présenté une petite partie du module NumPy, mais vous avez pu en constater son extraordinaire puissance. On pourrait au premier abord être tenté d'abandonner les listes, toutefois elles gardent toute leur importance. Alors, quand utiliser les listes ou quand utiliser les arrays NumPy ? Voici une liste non exhaustive d'éléments qui peuvent guider votre choix :

Utilisez NumPy pour :

• les opérations vectorielles (éléments par éléments) ;
• lorsque vous souhaitez manipuler des objets mathématiques (vecteurs, matrices, etc.) et les outils associés (algèbre linéaire) ;
• tout ce qui est numérique de manière générale.

Utilisez les listes :

• Lorsque vous avez besoin d'un conteneur pour accumuler des valeurs (fussent-elles des sous-listes), surtout lorsqu'elles ne sont pas homogènes (c'est-à-dire du même type).
• Lorsque vous souhaitez accumuler des valeurs au fur et à mesure des itérations d'une boucle. Pour cela, la méthode .append() des listes est bien plus efficace que de faire grandir un array ligne par ligne (c'est-à-dire en ajoutant une ligne avec np.concatenate() à chaque itération).
• Lorsqu'on ne peut pas utiliser les fonctions de lecture de fichier de NumPy pour quelque raison que ce soit, il est tout à fait classique de faire grandir une liste au fur et à mesure de la lecture du fichier puis de la convertir à la fin en array. De manière générale, utilisez np.concatenate() seulement pour concaténer des gros arrays, pas pour ajouter une seule ligne.

Enfin, comme nous vous le conseillons depuis le début, soignez votre documentation (docstrings) et vos commentaires lorsque vous utilisez des arrays. NumPy permet de réaliser des opérations vectorielles de manière très compacte. Il est donc essentiel de se mettre à la place du lecteur de votre script (y compris vous dans quelques semaines ou mois) et de documenter ce que contient chaque array ainsi que sa dimensionnalité (1D, 2D, etc.).

Le module NumPy est la brique de base du calcul numérique en Python. Associé aux modules SciPy et matplotlib, ainsi qu'aux notebooks Jupyter (voir le chapitre précédent), il permet de faire du calcul scientifique de manière très efficace. On verra dans le chapitre 22 Module Pandas que la puissance de NumPy est également utilisée par le module pandas pour faire de l'analyse de données.

Pour aller plus loin

• Le livre de Nicolas Rougier From Python to Numpy est une excellente ressource pour explorer plus en détails les possibilités de NumPy.
• Les tutoriels proposés par les développeurs de NumPy sont également un bon moyen de poursuivre votre exploration de cette bibliothèque incontournable en sciences.

20.11 Exercices

Conseils

Pour ces exercices, utilisez des notebooks Jupyter.

20.11.1 Nombres pairs et impairs

Soit impairs un array NumPy qui contient les nombres :

1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21

En une seule instruction, construisez l'array pairs dans lequel tous les éléments de impairs sont incrémentés de 1. Comparez ce que vous venez de faire avec l'exercice « Nombres pairs et impairs » du chapitre 5 Boucles et comparaisons.

20.11.2 Distance entre deux atomes carbones alpha consécutifs de la barstar

La barstar est un inhibiteur de ribonucléase. C'est une protéine relativement simple qui contient 89 acides aminés. Sa structure tridimensionnelle, obtenue par résonance magnétique nucléaire (RMN), se trouve dans la Protein Data Bank (PDB) sous le code 1BTA.

L'objectif de cet exercice est de calculer la distance entre carbones alpha consécutifs le long de la chaîne peptidique avec module NumPy et de découvrir une anomalie.

Le morceau de code suivant vous sera utile pour extraire les coordonnées atomiques des carbones alpha de la barstar depuis un fichier PDB :

with open("1bta.pdb", "r") as f_pdb, open("1bta_CA.txt", "w") as f_CA:
    for ligne in f_pdb:
        if ligne.startswith("ATOM") and ligne[12:16].strip() == "CA":
            x = ligne[30:38]
            y = ligne[38:46]
            z = ligne[46:54]
            f_CA.write(f"{x} {y} {z} ")

• Ligne 1. On ouvre deux fichiers simultanément. Ici, le fichier 1bta.pdb est ouvert en lecture (r) et le fichier 1bta_CA.txt est ouvert en écriture (w).
• Pour chaque ligne du fichier PDB (ligne 2), si la ligne débute par ATOM et le nom de l'atome est CA (ligne 3), alors on extrait les coordonnées atomiques (lignes 4 à 6) et on les écrit dans le fichier 1bta_CA.txt (ligne 7). Les coordonnées sont toutes enregistrées sur une seule ligne, les unes après les autres.

Voici les étapes à suivre :

1. Extraction des coordonnées atomiques

   • Téléchargez le fichier 1bta.pdb qui correspond à la structure de la barstar sur le site de la PDB (lien direct vers le fichier).
   • Utilisez le code précédent pour extraire les coordonnées atomiques des carbones alpha de la barstar.

2. Lecture des coordonnées

   • Ouvrez le fichier 1bta_CA.txt avec Python et créez une liste contenant toutes les coordonnées sous forme de floats avec les fonctions split() et float().
   • Affichez à l'écran le nombre total de coordonnées.

3. Construction de la matrice de coordonnées

   • En ouvrant dans un éditeur de texte le fichier 1bta.pdb, trouvez le nombre d'acides aminés qui constituent la barstar.
   • Avec la fonction array() du module NumPy, convertissez la liste de coordonnées en array. Avec la fonction reshape() de NumPy, construisez ensuite une matrice à deux dimensions contenant les coordonnées des carbones alpha de la barstar. Affichez les dimensions de cette matrice.

4. Calcul de la distance

   • Créez maintenant une matrice qui contient les coordonnées des \(n-1\) premiers carbones alpha et une autre qui contient les coordonnées des \(n-1\) derniers carbones alpha. Affichez les dimensions des matrices pour vérification.
   • En utilisant les opérateurs mathématiques habituels (-, +, **2) et les fonctions sqrt() et sum() du module NumPy, calculez la distance entre les atomes \(n\) et \(n+1\).
   • Pour chaque atome, affichez le numéro de l'atome et la distance entre carbones alpha consécutifs avec un chiffre après la virgule. Repérez la valeur surprenante.

20.11.3 Jour le plus chaud

Le fichier temperature.dat contient un relevé de quatre températures pour chaque jour de la semaine :

Lun 12 11 14 12
Mar 12 10 14 11
Mer 11 11 14 13
[...]

À l'aide du module NumPy, on souhaite déterminer quel est le jour de la semaine le plus chaud. Pour cela nous vous proposons les étapes suivantes :

1. Récupérez le nom des jours de la semaine depuis le fichier et stockez-les dans une liste days.
2. Récupérez les valeurs de températures depuis le fichier et stockez-les dans un array 2D. La fonction np.loadtxt() et son argument usecols vous seront utiles.
3. Parcourez chaque ligne de la matrice, calculez la température moyenne de chaque jour puis stockez-la dans une liste mean_temps.
4. À l'aide des deux listes days et mean_temps, déterminez et affichez le jour le plus chaud.

20.11.4 Calcul du centre de masse d'une membrane

L'image de gauche de la figure 2 montre le cliché d'une membrane de POPC (cyan) entourée d'eau (bleu) (coordonnées trouvées ici). Les atomes de phosphore des groupes phosphates sont représentés en boule de van der Waals brune. Dans cet exercice, on cherche à calculer le centre de masse de la membrane, ainsi que le centre de masse (COM) de chaque monocouche de phosphores. Ces COM sont représentés sous forme de croix dans le graphique de droite de la figure 2.

Figure 2. Cliché d'une membrane de POPC.

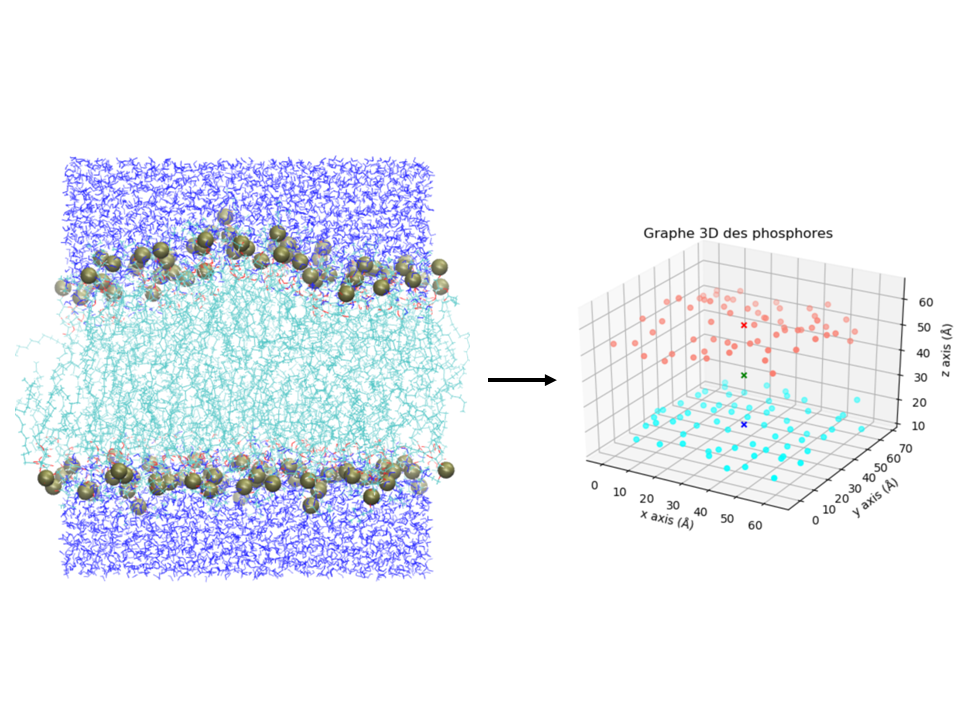
Les coordonnées cartésiennes \((x, y, z)\) de chaque atome de phosphore (en Å) sont stockées dans le fichier coors_P.dat, à raison d'un atome par ligne.

Nous vous proposons les étapes suivantes pour résoudre cet exercice à l'aide du module NumPy :

1. Récupérez les coordonnées des atomes de phosphore depuis le fichier coors_P.dat et stockez-les dans un array 2D (matrice) coors_P. La dimensionnalité de cette matrice est \(n \times 3\), avec \(n\) le nombre de phosphores.
2. Calculez le \(z\) moyen de tous les phosphores (nombre réel) et stockez-le dans la variable mean_z. La méthode .mean() vous sera utile.
3. Avec des masques de booléens, récupérez les coordonnées des phosphores de la monocouche du haut dans un array 2D upper. Faites de même avec la monocouche du bas dans un array 2D lower.
4. Calculez le centre de masse COM de la membrane, ainsi que de la monocouche du haut COM_upper et du bas COM_lower. Pensez aux méthodes de calcul sur les arrays et l'argument axis.
5. Une fois tout cela effectué, créez un graphique 3D pour représenter les différents centres de masse. Utilisez la fonction scatter() du module matplotlib pour l'affichage en 3D. Voici un squelette de programme pour vous aider :

# Initialisation du graphique.
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
fig = plt.figure()                       
ax = fig.add_subplot(111, projection="3d")
[...]
# X, Y et Z sont des arrays 1D de n éléments.
# Par exemple X représente tous les x des P de la monocouche upper.
[...]
# Affichage de la couche upper.
ax.scatter(X, Y, Z, c="salmon", marker="o")
# Affichage du COM de la couche upper.
ax.scatter(x, y, z, c="red", marker="x")
[...]
# Affichage des étiquettes des axes et du titre.
ax.set_xlabel("x (Å)")
ax.set_ylabel("y (Å)")
ax.set_zlabel("z (Å)")
ax.set_title("Graphe 3D des phosphores")
plt.show()