5 Boucles et comparaisons

5.1 Boucles for

5.1.1 Principe

En programmation, on est souvent amené à répéter plusieurs fois une instruction. Incontournables à tout langage de programmation, les boucles vont nous aider à réaliser cette tâche répétitive de manière compacte et efficace.

Imaginez par exemple que vous souhaitiez afficher les éléments d'une liste les uns après les autres. Dans l'état actuel de vos connaissances, il faudrait taper quelque chose du style :

animaux = ["girafe", "tigre", "singe", "souris"]
print(animaux[0])
print(animaux[1])
print(animaux[2])
print(animaux[3])

Si votre liste ne contient que 4 éléments, ceci est encore faisable mais imaginez qu'elle en contienne 100 voire 1 000 ! Pour remédier à cela, il faut utiliser les boucles . Regardez l'exemple suivant :

>>> animaux = ["girafe", "tigre", "singe", "souris"]
>>> for animal in animaux:
...     print(animal)
...
girafe
tigre
singe
souris

Commentons en détails ce qu'il s'est passé dans cet exemple :

La variable animal est appelée variable d'itération , elle prend successivement les différentes valeurs de la liste animaux à chaque itérations (ou tour) de boucle. On verra un peu plus loin dans ce chapitre que l'on peut choisir le nom que l'on veut pour cette variable. Celle-ci est créée par Python la première fois que la ligne contenant le for est exécutée (si elle existait déjà son contenu serait écrasé). Une fois la boucle terminée, cette variable d'itération animal n'est pas détruite et conserve la dernière valeur de la liste animaux (ici la chaîne de caractères "souris").

Notez bien les types des variables utilisées ici :

• animaux est une liste sur laquelle on itère ;
• animal est une chaîne de caractères car chaque élément de la liste animaux est une chaîne de caractères.

Nous verrons plus loin que la variable d'itération peut être de n'importe quel type selon la liste parcourue. En Python, une boucle itère la plupart du temps sur un objet dit séquentiel (c'est-à-dire un objet constitué d'autres objets) tel qu'une liste. De tels objets sont dits itérables car on peut effectuer une boucle dessus. Nous verrons aussi plus tard d'autres objets séquentiels sur lesquels on peut itérer dans une boucle.

D'ores et déjà, prêtez attention au caractère deux-points « : » à la fin de la ligne débutant par for. Cela signifie que la boucle for attend un bloc d'instructions, en l’occurrence toutes les instructions que Python répétera à chaque itération de la boucle. On appelle ce bloc d'instructions le corps de la boucle. Comment indique-t-on à Python où ce bloc commence et se termine ? Cela est signalé uniquement par l'indentation, c'est-à-dire le décalage vers la droite de la (ou des) ligne(s) du bloc d'instructions.

Remarque

Les notions de bloc d'instruction et d'indentations ont été introduites dans le chapitre 1 Introduction.

Dans l'exemple suivant, le corps de la boucle contient deux instructions (ligne 2 et ligne 3) car elles sont indentées par rapport à la ligne débutant par for :

for animal in animaux:
    print(animal)
    print(animal*2)
print("C'est fini")

La ligne 4 ne fait pas partie du corps de la boucle car elle est au même niveau que le for (c'est-à-dire non indentée par rapport au for). Notez également que chaque instruction du corps de la boucle doit être indentée de la même manière (ici 4 espaces).

Remarque

Outre une meilleure lisibilité, les deux-points et l'indentation sont formellement requis en Python. Même si on peut indenter comme on veut (plusieurs espaces ou plusieurs tabulations, mais pas une combinaison des deux), les développeurs recommandent l'utilisation de quatre espaces. Vous pouvez consulter à ce sujet le chapitre 16 Bonnes pratiques de programmation en Python.

Faites en sorte de configurer votre éditeur de texte favori de façon à écrire quatre espaces lorsque vous tapez sur la touche Tab (tabulation).

Si on oublie l'indentation, Python renvoie un message d'erreur :

>>> for animal in animaux:
... print(animal)
  File "<stdin>", line 2
    print(animal)
        ^
IndentationError: expected an indented block

Dans les exemples ci-dessus, nous avons exécuté une boucle en itérant directement sur une liste. Une tranche d'une liste étant elle même une liste, on peut également itérer dessus :

>>> animaux = ["girafe", "tigre", "singe", "souris"]
>>> for animal in animaux[1:3]:
...     print(animal)
...
tigre
singe

On a vu que les boucles for pouvaient utiliser une liste contenant des chaînes de caractères, mais elles peuvent tout aussi bien utiliser des listes contenant des entiers (ou n'importe quel type de variable) :

>>> for i in [1, 2, 3]:
...     print(i)
...
1
2
3

5.1.2 Fonction range()

Python possède la fonction range() que nous avons rencontrée précédemment dans le chapitre 4 Listes, pratique pour faire une boucle sur une liste d'entiers de manière automatique :

>>> for i in range(4):
...     print(i)
...
0
1
2
3

Dans cet exemple, nous pouvons faire plusieurs remarques importantes :

• Contrairement à la création de liste avec list(range(4)), la fonction range() peut être utilisée telle quelle dans une boucle. Il n'est pas nécessaire de taper for i in list(range(4)): même si cela fonctionnerait également.

• Comment cela est possible ? range() est une fonction qui a été spécialement conçue pour cela, c'est-à-dire que l'on peut itérer directement dessus. Pour Python, il s'agit d'un nouveau type : par exemple dans l'instruction x = range(3), la variable x est de type range (tout comme on avait les types int, float, str ou list) à utiliser spécialement avec les boucles.

• L'instruction list(range(4)) se contente de transformer un objet de type range en un objet de type list. Si vous vous souvenez bien, il s'agit d'une fonction de casting, qui convertit un type en un autre (voir chapitre 2 Variables). Il n'y aucun intérêt à utiliser dans une boucle la construction for i in list(range(4)):. C'est même contre-productif. En effet, range() se contente de stocker l'entier actuel, le pas pour passer à l'entier suivant, et le dernier entier à parcourir, ce qui revient à stocker seulement 3 nombres entiers et ce quelle que soit la longueur de la séquence, même avec un range(1000000). Si on utilisait list(range(1000000)), Python construirait d'abord une liste de 1 million d'éléments dans la mémoire puis itérerait dessus, d'où une énorme perte de temps !

5.1.3 Nommage de la variable d'itération

Dans l'exemple précédent, nous avons choisi le nom i pour la variable d'itération. Ceci est une habitude en informatique et indique en général qu'il s'agit d'un entier (le nom i vient sans doute du mot indice ou index en anglais). Nous vous conseillons de suivre cette convention afin d'éviter les confusions. Si vous itérez sur les indices, vous pouvez appeler la variable d'itération i (par exemple dans for i in range(4):).

Si, par contre, vous itérez sur une liste comportant des chaînes de caractères (ou tout autre type de variable), utilisez un nom explicite pour la variable d'itération. Par exemple :

for prenom in ["Joe", "Bill", "John"]:

ou

for proportion in [0.12, 0.53, 0.07, 0.28]:

5.1.4 Itération sur les indices ou les éléments

Revenons à notre liste animaux. Nous allons maintenant parcourir cette liste, mais cette fois par une itération sur ses indices :

>>> animaux = ["girafe", "tigre", "singe", "souris"]
>>> for i in range(4):
...     print(animaux[i])
...
girafe
tigre
singe
souris

La variable i prendra les valeurs successives 0, 1, 2 et 3 et on accèdera à chaque élément de la liste animaux par son indice (i.e. animaux[i]). Notez à nouveau le nom i de la variable d'itération car on itère sur les indices.

Quand utiliser l'une ou l'autre des deux méthodes ? La plus efficace est celle qui réalise les itérations directement sur les éléments :

>>> animaux = ["girafe", "tigre", "singe", "souris"]
>>> for animal in animaux:
...     print(animal)
...
girafe
tigre
singe
souris

Remarque

Dans le chapitre 18 Jupyter et ses notebooks, nous mesurerons le temps d'exécution de ces deux méthodes pour vous montrer que l'itération sur les éléments est la méthode la plus rapide.

Toutefois, il se peut qu'au cours d'une boucle vous ayez besoin des indices, auquel cas vous devrez itérer sur les indices :

>>> animaux = ["girafe", "tigre", "singe", "souris"]
>>> for i in range(len(animaux)):
...     print(f"L'animal {i} est un(e) {animaux[i]}")
...
L'animal 0 est un(e) girafe
L'animal 1 est un(e) tigre
L'animal 2 est un(e) singe
L'animal 3 est un(e) souris

Enfin, Python possède la fonction enumerate() qui vous permet d'itérer sur les indices et les éléments eux-mêmes :

>>> animaux = ["girafe", "tigre", "singe", "souris"]
>>> for i, animal in enumerate(animaux):
...     print(f"L'animal {i} est un(e) {animal}")
...
L'animal 0 est un(e) girafe
L'animal 1 est un(e) tigre
L'animal 2 est un(e) singe
L'animal 3 est un(e) souris

5.2 Comparaisons

Avant de passer aux boucles while, abordons tout de suite les comparaisons. Celles-ci seront reprises dans le chapitre 6 Tests.

Python est capable d'effectuer toute une série de comparaisons entre le contenu de deux variables, telles que :

Opérateur de comparaison	Signification
==	égal à
!=	différent de
>	strictement supérieur à
>=	supérieur ou égal à
<	strictement inférieur à
<=	inférieur ou égal à

Observez les exemples suivants avec des nombres entiers :

>>> x = 5
>>> x == 5
True
>>> x > 10
False
>>> x < 10
True

Python renvoie la valeur True si la comparaison est vraie et False si elle est fausse. True et False sont des booléens comme nous avions vu au chapitre 2 Variables.

Faites bien attention à ne pas confondre l'opérateur d'affectation = qui affecte une valeur à une variable et l'opérateur de comparaison == qui compare les valeurs de deux variables.

Vous pouvez également effectuer des comparaisons sur des chaînes de caractères.

>>> animal = "tigre"
>>> animal == "tig"
False
>>> animal != "tig"
True
>>> animal == "tigre"
True

Dans le cas des chaînes de caractères, a priori seuls les tests == et != ont un sens. En fait, on peut aussi utiliser les opérateurs <, >, <= et >=. Dans ce cas, l'ordre alphabétique est pris en compte, par exemple :

>>> "a" < "b"
True

"a" est inférieur à "b" car le caractère a est situé avant le caractère b dans l'ordre alphabétique. En fait, c'est l'ordre ASCII des caractères qui est pris en compte (à chaque caractère correspond un code numérique), on peut donc aussi comparer des caractères spéciaux (comme # ou ~) entre eux. Enfin, on peut comparer des chaînes de caractères de plusieurs caractères :

>>> "ali" < "alo"
True
>>> "abb" < "ada"
True

Dans ce cas, Python compare les deux chaînes de caractères, caractère par caractère, de la gauche vers la droite (le premier caractère avec le premier, le deuxième avec le deuxième, etc). Dès qu'un caractère est différent entre l'une et l'autre des deux chaînes, il considère que la chaîne la plus petite est celle qui présente le caractère ayant le plus petit code ASCII (les caractères suivants de la chaîne de caractères sont ignorés dans la comparaison), comme dans l'exemple "abb" < "ada" ci-dessus.

5.3 Boucles while

Une alternative à l'instruction for couramment utilisée en informatique est la boucle while. Avec ce type de boucle, une série d'instructions est exécutée tant qu'une condition est vraie. Par exemple :

>>> i = 1
>>> while i <= 4:
...     print(i)
...     i = i + 1
...
1
2
3
4

Remarquez qu'il est encore une fois nécessaire d'indenter le bloc d'instructions correspondant au corps de la boucle (ici, les instructions lignes 3 et 4).

Une boucle while nécessite généralement trois éléments pour fonctionner correctement :

1. Initialisation de la variable d'itération avant la boucle (ligne 1).
2. Test de la variable d'itération associée à l'instruction while (ligne 2).
3. Mise à jour de la variable d'itération dans le corps de la boucle (ligne 4).

Faites bien attention aux tests et à l'incrémentation que vous utilisez, car une erreur mène souvent à des « boucles infinies » qui ne s'arrêtent jamais. Vous pouvez néanmoins toujours stopper l'exécution d'un script Python à l'aide de la combinaison de touches Ctrl-C (c'est-à-dire en pressant simultanément les touches Ctrl et C). Par exemple :

i = 0
while i < 10:
    print("Le Python c'est cool !")

Ici, nous avons omis de mettre à jour la variable i dans le corps de la boucle. Par conséquent, la boucle ne s'arrêtera jamais (sauf en pressant Ctrl-C) puisque la condition i < 10 sera toujours vraie.

La boucle while combinée à la fonction input() peut s'avérer commode lorsqu'on souhaite demander à l'utilisateur une valeur numérique. Par exemple :

>>> i = 0
>>> while i < 10:
...     reponse = input("Entrez un entier supérieur à 10 : ")
...     i = int(reponse)
...
Entrez un entier supérieur à 10 : 4
Entrez un entier supérieur à 10 : -3
Entrez un entier supérieur à 10 : 15
>>> i
15

La fonction input() prend en argument un message (sous la forme d'une chaîne de caractères), demande à l'utilisateur d'entrer une valeur et renvoie celle-ci sous forme d'une chaîne de caractères, qu'il faut ensuite convertir en entier (avec la fonction int() ligne 4). Si on reprend les trois éléments d'une boucle while, on trouve l'initialisation de la variable d'itération en ligne 1, le test de sa valeur en ligne 2, et sa mise à jour en ligne 4.

Conseils

Comment choisir entre la boucle while et la boucle for ? La boucle while s'utilisera généralement lorsqu'on ne sait pas à l'avance le nombre d'itérations (comme dans le dernier exemple). Si on connait à l'avance le nombre d'itérations, par exemple si on veut écrire 10 fois Le Python c'est cool, nous vous conseillons la boucle for.

5.4 Exercices

Conseils

Pour ces exercices, créez des scripts puis exécutez-les dans un shell.

5.4.1 Boucles de base

Soit la liste ["vache", "souris", "levure", "bacterie"]. Affichez l'ensemble des éléments de cette liste (un élément par ligne) de trois façons différentes (deux méthodes avec for et une avec while).

5.4.2 Boucles et jours de la semaine

Constituez une liste semaine contenant les 7 jours de la semaine.

Écrivez une série d'instructions affichant les jours de la semaine (en utilisant une boucle for), ainsi qu'une autre série d'instructions affichant les jours du week-end (en utilisant une boucle while).

5.4.3 Nombres de 1 à 10 sur une ligne

Avec une boucle, affichez les nombres de 1 à 10 sur une seule ligne.

Conseils

Pensez à relire le début du chapitre 3 Affichage qui discute de la fonction print().

5.4.4 Nombres pairs et impairs

Soit impairs la liste de nombres [1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21]. Écrivez un programme qui, à partir de la liste impairs, construit une liste pairs dans laquelle tous les éléments de impairs sont incrémentés de 1.

5.4.5 Calcul de la moyenne

Voici les notes d'un étudiant [14, 9, 6, 8, 12]. Calculez la moyenne de ces notes. Utilisez l'écriture formatée pour afficher la valeur de la moyenne avec deux décimales.

5.4.6 Produit de nombres consécutifs

Avec les fonctions list() et range(), créez la liste entiers contenant les nombres entiers pairs de 2 à 20 inclus.

Calculez ensuite le produit des nombres consécutifs deux à deux de entiers en utilisant une boucle. Exemple pour les premières itérations :

8
24
48
[...]

5.4.7 Triangle

Créez un script qui dessine un triangle comme celui-ci :

*
**
***
****
*****
******
*******
********
*********
**********

5.4.8 Triangle inversé

Créez un script qui dessine un triangle comme celui-ci :

**********
*********
********
*******
******
*****
****
***
**
*

5.4.9 Triangle gauche

Créez un script qui dessine un triangle comme celui-ci :

         *
        **
       ***
      ****
     *****
    ******
   *******
  ********
 *********
**********

5.4.10 Pyramide

Créez un script pyra.py qui dessine une pyramide comme celle-ci :

         *
        ***
       *****
      *******
     *********
    ***********
   *************
  ***************
 *****************
*******************

Essayez de faire évoluer votre script pour dessiner la pyramide à partir d'un nombre arbitraire de lignes N. Vous pourrez demander à l'utilisateur le nombre de lignes de la pyramide avec les instructions suivantes qui utilisent la fonction input() :

reponse = input("Entrez un nombre de lignes (entier positif): ")
N = int(reponse)

5.4.11 Parcours de matrice

Imaginons que l'on souhaite parcourir tous les éléments d'une matrice carrée, c'est-à-dire d'une matrice qui est constituée d'autant de lignes que de colonnes.

Créez un script qui parcourt chaque élément de la matrice et qui affiche le numéro de ligne et de colonne uniquement avec des boucles for.

Pour une matrice de dimensions 2 \(\times\) 2, le schéma de la figure 1 vous indique comment parcourir une telle matrice. L'affichage attendu est :

ligne colonne
   1    1
   1    2
   2    1
   2    2

Figure 1. Parcours d'une matrice.

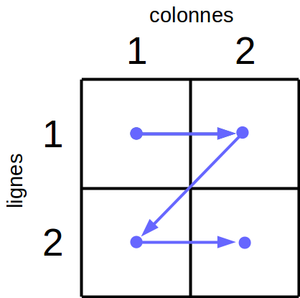
Attention à bien respecter l'alignement des chiffres qui doit être justifié à droite sur 4 caractères. Testez avec une matrice de dimensions 3 \(\times\) 3, puis 5 \(\times\) 5, et enfin 10 \(\times\) 10.

Créez une seconde version de votre script, cette fois-ci avec deux boucles while.

5.4.12 Parcours de demi-matrice sans la diagonale (exercice ++)

En se basant sur le script précédent, on souhaite réaliser le parcours d'une demi-matrice carrée sans la diagonale. On peut noter que cela produit tous les couples possibles une seule fois (1 et 2 est équivalent à 2 et 1), en excluant par ailleurs chaque élément avec lui même (1 et 1, 2 et 2, etc). Pour mieux comprendre ce qui est demandé, la figure 2 indique les cases à parcourir en gris :

Figure 2. Demi-matrice sans la diagonale (en gris).

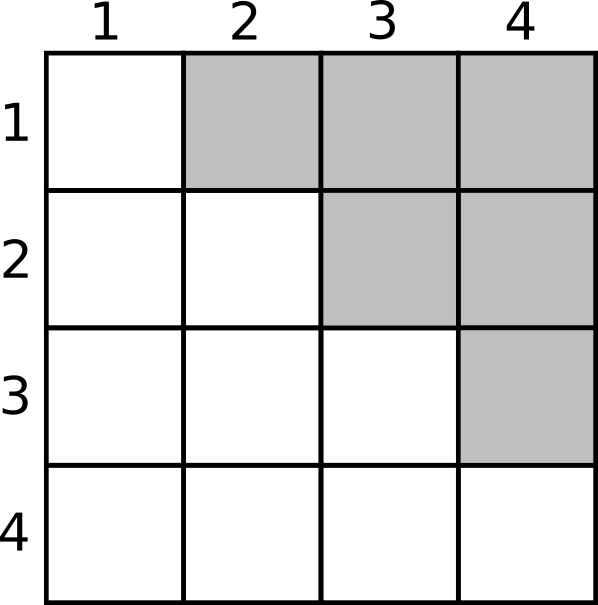
Créez un script qui affiche le numéro de ligne et de colonne, puis la taille de la matrice \(N \times N\) et le nombre total de cases parcourues. Par exemple pour une matrice 4 \(\times\) 4 (N=4) :

ligne colonne
   1    2
   1    3
   1    4
   2    3
   2    4
   3    4
Pour une matrice 4x4, on a parcouru 6 cases

Testez votre script avec N=3, puis N=4 et enfin N=5.

Concevez une seconde version à partir du script précédent, où cette fois on n'affiche plus tous les couples possibles, mais simplement la valeur de N et le nombre de cases parcourues. Affichez cela pour des valeurs de N allant de 2 à 10.

Pouvez-vous trouver une formule générale reliant le nombre de cases parcourues à N ?

5.4.13 Sauts de puce

On imagine une puce qui se déplace aléatoirement sur une ligne, en avant ou en arrière, par pas de 1 ou -1. Par exemple, si elle est à l'emplacement 0, elle peut sauter à l'emplacement 1 ou -1 ; si elle est à l'emplacement 2, elle peut sauter à l'emplacement 3 ou 1, etc.

Avec une boucle while, simulez le mouvement de cette puce de l'emplacement initial 0 à l'emplacement final 5 (voir le schéma de la figure 3). Combien de sauts sont nécessaires pour réaliser ce parcours ? Relancez plusieurs fois le programme. Trouvez-vous le même nombre de sauts à chaque exécution ?

Figure 3. Sauts de puce.

Conseils

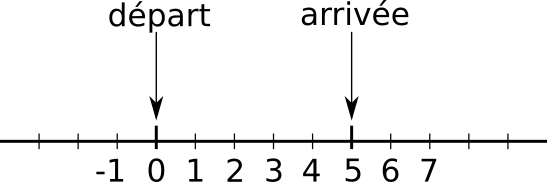
Utilisez l'instruction random.choice([-1,1]) qui renvoie au hasard les valeurs -1 ou 1 avec la même probabilité. Avant d'utiliser cette instruction, mettez au tout début de votre script la ligne
import random
Nous verrons la signification de cette syntaxe particulière dans le chapitre 9 Modules.

5.4.14 Suite de Fibonacci (exercice +++)

La suite de Fibonacci est une suite mathématique qui porte le nom de Leonardo Fibonacci, un mathématicien italien du XIII\(^{\rm e}\) siècle. Initialement, cette suite a été conçue pour décrire la croissance d'une population de lapins, mais elle peut également être utilisée pour décrire certains motifs géométriques retrouvés dans la nature (coquillages, fleurs de tournesol...).

Pour la suite de Fibonacci \((x_n)\), le terme au rang n (avec \(n > 1\)) est la somme des nombres aux rangs \(n - 1\) et \(n - 2\) :

\(x_n = x_{n-1} + x_{n-2}\)

Par définition, les deux premiers termes sont \(x_0 = 0\) et \(x_1 = 1\).

À titre d'exemple, les 10 premiers termes de la suite de Fibonacci sont donc 0, 1, 1, 2, 3, 5, 8, 13, 21 et 34.

Créez un script qui construit une liste fibo avec les 15 premiers termes de la suite de Fibonacci puis l'affiche.

Améliorez ce script en affichant, pour chaque élément de la liste fibo avec \(n > 1\), le rapport entre l'élément de rang \(n\) et l'élément de rang \(n - 1\). Ce rapport tend-il vers une constante ? Si oui, laquelle ?